

The slope of the standard curve by linear regression was $\beta_1$, and the standard deviation about the regression for the standard curve was: $$s_r=\sqrt+D_0$, the estimated value, as one would expect of a genuine confidence limit.
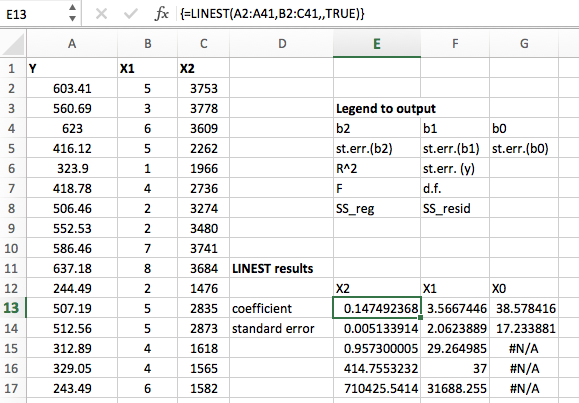
Say that you generate a standard curve with known values of $x$ and measured values of $y$. The same result is provided in equation 5.25 of an online analytical chemistry textbook that I find more generally useful and of whose content you should, as a chemist, be aware. If what you care about is the SD of a prediction of $x$ given a value of $y$, then what you should examine is the square root of equation (10) of the linked reference. Your dream of a "global SD" for estimated errors in $x$ given a value of $y$ is not possible.


 0 kommentar(er)
0 kommentar(er)
